Complementary Filters Shaping Using \(\mathcal{H}_\infty\) Synthesis - Tikz Figures

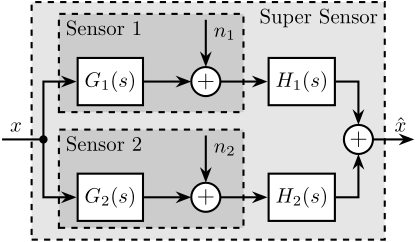
1. Fig 1: Sensor Fusion Architecture
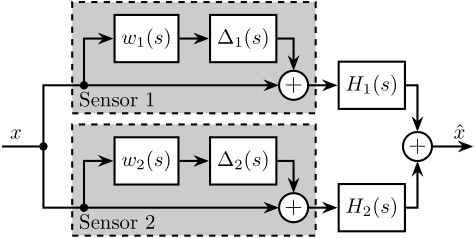
2. Fig 2: Sensor fusion architecture with sensor dynamics uncertainty
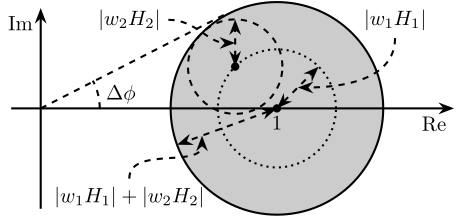
3. Fig 3: Uncertainty set of the super sensor dynamics
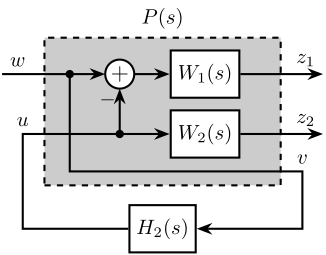
4. Fig 4: Architecture used for \(\mathcal{H}_\infty\) synthesis of complementary filters
5. Fig 5: Magnitude of a weighting function generated using the proposed formula
6. Fig 6: Frequency response of the weighting functions and complementary filters obtained using \(\mathcal{H}_\infty\) synthesis
7. Fig 7: Architecture for \(\mathcal{H}_\infty\) synthesis of three complementary filters
8. Fig 8: Frequency response of the weighting functions and three complementary filters obtained using \(\mathcal{H}_\infty\) synthesis
9. Fig 9: Specifications and weighting functions magnitude used for \(\mathcal{H}_\infty\) synthesis
10. Fig 10: Comparison of the FIR filters (solid) with the filters obtained with \(\mathcal{H}_\infty\) synthesis (dashed)

Configuration file is accessible here.

1 Fig 1: Sensor Fusion Architecture

\begin{tikzpicture}
  \node[branch] (x) at (0, 0);
  \node[block, above right=0.5 and 0.5 of x](G1){$G_1(s)$};
  \node[block, below right=0.5 and 0.5 of x](G2){$G_2(s)$};
  \node[addb, right=0.8 of G1](add1){};
  \node[addb, right=0.8 of G2](add2){};
  \node[block, right=0.8 of add1](H1){$H_1(s)$};
  \node[block, right=0.8 of add2](H2){$H_2(s)$};
  \node[addb, right=5 of x](add){};

  \draw[] ($(x)+(-0.7, 0)$) node[above right]{$x$} -- (x.center);
  \draw[->] (x.center) |- (G1.west);
  \draw[->] (x.center) |- (G2.west);
  \draw[->] (G1.east) -- (add1.west);
  \draw[->] (G2.east) -- (add2.west);
  \draw[<-] (add1.north) -- ++(0, 0.8)node[below right](n1){$n_1$};
  \draw[<-] (add2.north) -- ++(0, 0.8)node[below right](n2){$n_2$};
  \draw[->] (add1.east) -- (H1.west);
  \draw[->] (add2.east) -- (H2.west);
  \draw[->] (H1) -| (add.north);
  \draw[->] (H2) -| (add.south);
  \draw[->] (add.east) -- ++(0.7, 0) node[above left]{$\hat{x}$};

  \begin{scope}[on background layer]
    \node[fit={($(G2.south-|x)+(-0.2, -0.3)$) ($(n1.north east-|add.east)+(0.2, 0.3)$)}, fill=black!10!white, draw, dashed, inner sep=0pt] (supersensor) {};
    \node[below left] at (supersensor.north east) {Super Sensor};

    \node[fit={($(G1.south west)+(-0.3, -0.1)$) ($(n1.north east)+(0.0, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor1) {};
    \node[below right] at (sensor1.north west) {Sensor 1};
    \node[fit={($(G2.south west)+(-0.3, -0.1)$) ($(n2.north east)+(0.0, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor2) {};
    \node[below right] at (sensor2.north west) {Sensor 2};
  \end{scope}
\end{tikzpicture}

Figure 1: Sensor Fusion Architecture (png, pdf, tex).

2 Fig 2: Sensor fusion architecture with sensor dynamics uncertainty

\begin{tikzpicture}
  \node[branch] (x) at (0, 0);
  \node[addb, above right=0.8 and 4 of x](add1){};
  \node[addb, below right=0.8 and 4 of x](add2){};
  \node[block, above left=0.2 and 0.1 of add1](delta1){$\Delta_1(s)$};
  \node[block, above left=0.2 and 0.1 of add2](delta2){$\Delta_2(s)$};
  \node[block, left=0.5 of delta1](W1){$w_1(s)$};
  \node[block, left=0.5 of delta2](W2){$w_2(s)$};
  \node[block, right=0.5 of add1](H1){$H_1(s)$};
  \node[block, right=0.5 of add2](H2){$H_2(s)$};
  \node[addb, right=6 of x](add){};

  \draw[] ($(x)+(-0.7, 0)$) node[above right]{$x$} -- (x.center);
  \draw[->] (x.center) |- (add1.west);
  \draw[->] (x.center) |- (add2.west);
  \draw[->] ($(add1-|W1.west)+(-0.5, 0)$)node[branch](S1){} |- (W1.west);
  \draw[->] ($(add2-|W2.west)+(-0.5, 0)$)node[branch](S1){} |- (W2.west);
  \draw[->] (W1.east) -- (delta1.west);
  \draw[->] (W2.east) -- (delta2.west);
  \draw[->] (delta1.east) -| (add1.north);
  \draw[->] (delta2.east) -| (add2.north);
  \draw[->] (add1.east) -- (H1.west);
  \draw[->] (add2.east) -- (H2.west);
  \draw[->] (H1.east) -| (add.north);
  \draw[->] (H2.east) -| (add.south);
  \draw[->] (add.east) -- ++(0.7, 0) node[above left]{$\hat{x}$};

  \begin{scope}[on background layer]
    \node[block, fit={($(W1.north-|S1)+(-0.2, 0.2)$) ($(add1.south east)+(0.2, -0.3)$)}, fill=black!20!white, dashed, inner sep=0pt] (sensor1) {};
    \node[above right] at (sensor1.south west) {Sensor 1};
    \node[block, fit={($(W2.north-|S1)+(-0.2, 0.2)$) ($(add2.south east)+(0.2, -0.3)$)}, fill=black!20!white, dashed, inner sep=0pt] (sensor2) {};
    \node[above right] at (sensor2.south west) {Sensor 2};
  \end{scope}
\end{tikzpicture}

Figure 2: Sensor fusion architecture with sensor dynamics uncertainty (png, pdf, tex).

3 Fig 3: Uncertainty set of the super sensor dynamics

\begin{tikzpicture}
  \begin{scope}[shift={(4, 0)}]

    % Uncertainty Circle
    \node[draw, circle, fill=black!20!white, minimum size=3.6cm] (c) at (0, 0) {};
    \path[draw, dotted] (0, 0) circle [radius=1.0];
    \path[draw, dashed] (135:1.0) circle [radius=0.8];

    % Center of Circle
    \node[below] at (0, 0){$1$};

    \draw[<->, dashed] (0, 0)   node[branch]{} -- coordinate[midway](r1) ++(45:1.0);
    \draw[<->, dashed] (135:1.0)node[branch]{} -- coordinate[midway](r2) ++(90:0.8);

    \node[] (l1) at (2, 1.5) {$|w_1 H_1|$};
    \draw[->, dashed, out=-90, in=0] (l1.south) to (r1);

    \node[] (l2) at (-2.5, 1.5) {$|w_2 H_2|$};
    \draw[->, dashed, out=0, in=-180] (l2.east) to (r2);

    \draw[<->, dashed] (0, 0) -- coordinate[near end](r3) ++(200:1.8);
    \node[] (l3) at (-2.5, -1.5) {$|w_1 H_1| + |w_2 H_2|$};
    \draw[->, dashed, out=90, in=-90] (l3.north) to (r3);
  \end{scope}

  % Real and Imaginary Axis
  \draw[->] (-0.5, 0) -- (7.0, 0) node[below left]{Re};
  \draw[->] (0, -1.7) -- (0, 1.7) node[below left]{Im};

  \draw[dashed] (0, 0) -- (tangent cs:node=c,point={(0, 0)},solution=2);
  \draw[dashed] (1, 0) arc (0:28:1) node[midway, right]{$\Delta \phi$};
\end{tikzpicture}

Figure 3: Uncertainty region of the super sensor dynamics in the complex plane (solid circle), of the sensor 1 (dotted circle) and of the sensor 2 (dashed circle) (png, pdf, tex).

4 Fig 4: Architecture used for \(\mathcal{H}_\infty\) synthesis of complementary filters

\begin{tikzpicture}
   \node[block={4.0cm}{2.5cm}, fill=black!20!white, dashed] (P) {};
   \node[above] at (P.north) {$P(s)$};

   \coordinate[] (inputw)  at ($(P.south west)!0.75!(P.north west) + (-0.7, 0)$);
   \coordinate[] (inputu)  at ($(P.south west)!0.35!(P.north west) + (-0.7, 0)$);

   \coordinate[] (output1) at ($(P.south east)!0.75!(P.north east) + ( 0.7, 0)$);
   \coordinate[] (output2) at ($(P.south east)!0.35!(P.north east) + ( 0.7, 0)$);
   \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east) + ( 0.7, 0)$);

   \node[block, left=1.4 of output1] (W1){$W_1(s)$};
   \node[block, left=1.4 of output2] (W2){$W_2(s)$};
   \node[addb={+}{}{}{}{-}, left=of W1] (sub) {};

   \node[block, below=0.3 of P] (H2) {$H_2(s)$};

   \draw[->] (inputw) node[above right]{$w$} -- (sub.west);
   \draw[->] (H2.west) -| ($(inputu)+(0.35, 0)$) node[above]{$u$} -- (W2.west);
   \draw[->] (inputu-|sub) node[branch]{} -- (sub.south);
   \draw[->] (sub.east) -- (W1.west);
   \draw[->] ($(sub.west)+(-0.6, 0)$) node[branch]{} |- ($(outputv)+(-0.35, 0)$) node[above]{$v$} |- (H2.east);
   \draw[->] (W1.east) -- (output1)node[above left]{$z_1$};
   \draw[->] (W2.east) -- (output2)node[above left]{$z_2$};
\end{tikzpicture}

Figure 4: Architecture used for \(\mathcal{H}_\infty\) synthesis of complementary filters (png, pdf, tex).

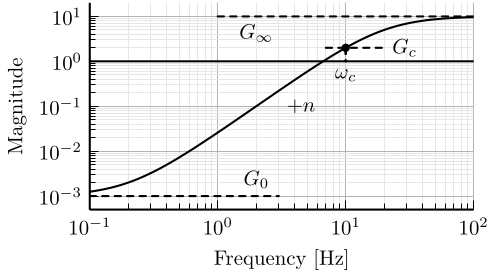
5 Fig 5: Magnitude of a weighting function generated using the proposed formula

\setlength\fwidth{6.5cm}
\setlength\fheight{3.5cm}

\begin{tikzpicture}
  \begin{axis}[%
    width=1.0\fwidth,
    height=1.0\fheight,
    at={(0.0\fwidth, 0.0\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.1,
    xmax=100,
    xtick={0.1,1,10, 100},
    xminorticks=true,
    ymode=log,
    ymin=0.0005,
    ymax=20,
    ytick={0.001, 0.01, 0.1, 1, 10},
    yminorticks=true,
    ylabel={Magnitude},
    xlabel={Frequency [Hz]},
    xminorgrids,
    yminorgrids,
    ]

    \addplot [color=black, line width=1.5pt, forget plot]
    table [x=freqs, y=ampl, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matweight_formula.csv};

    \addplot [color=black, dashed, line width=1.5pt]
    table[row sep=crcr]{%
      1     10\\
      100   10\\
    };
    \addplot [color=black, dashed, line width=1.5pt]
    table[row sep=crcr]{%
      0.1  0.001\\
      3    0.001\\
    };

    \addplot [color=black, line width=1.5pt]
    table[row sep=crcr]{%
      0.1  1\\
      100  1\\
    };

    \addplot [color=black, dashed, line width=1.5pt]
    table[row sep=crcr]{%
      10  2\\
      10  1\\
    };

    \node[below] at (2, 10) {$G_\infty$};
    \node[above] at (2, 0.001) {$G_0$};

    \node[branch] at (10, 2){};
    \draw[dashed, line cap=round] (7, 2) -- (20, 2) node[right]{$G_c$};
    \draw[dashed, line cap=round] (10, 2) -- (10, 1) node[below]{$\omega_c$};

    \node[right] at (3, 0.1) {$+n$};

  \end{axis}
\end{tikzpicture}

Figure 5: Magnitude of a weighting function generated using the proposed formula (png, pdf, tex).

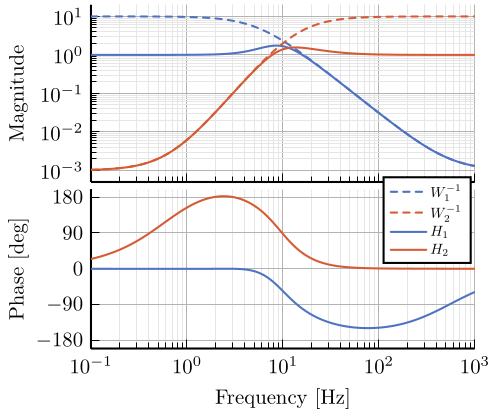
6 Fig 6: Frequency response of the weighting functions and complementary filters obtained using \(\mathcal{H}_\infty\) synthesis

\setlength\fwidth{6.5cm}
\setlength\fheight{6cm}

\begin{tikzpicture}
  \begin{axis}[%
    width=1.0\fwidth,
    height=0.5\fheight,
    at={(0.0\fwidth, 0.47\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.1,
    xmax=1000,
    xtick={0.1, 1, 10, 100, 1000},
    xticklabels={{}},
    xminorticks=true,
    ymode=log,
    ymin=0.0005,
    ymax=20,
    ytick={0.001, 0.01, 0.1, 1, 10},
    yminorticks=true,
    ylabel={Magnitude},
    xminorgrids,
    yminorgrids,
    ]
    \addplot [color=mycolor1, line width=1.5pt, forget plot]
    table [x=freqs, y=H1, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_filters_results.csv};

    \addplot [color=mycolor2, line width=1.5pt, forget plot]
    table [x=freqs, y=H2, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_filters_results.csv};

    \addplot [color=mycolor1, dashed, line width=1.5pt, forget plot]
    table [x=freqs, y=W1, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_weights.csv};

    \addplot [color=mycolor2, dashed, line width=1.5pt, forget plot]
    table [x=freqs, y=W2, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_weights.csv};
  \end{axis}

  \begin{axis}[%
    width=1.0\fwidth,
    height=0.45\fheight,
    at={(0.0\fwidth, 0.0\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.1,
    xmax=1000,
    xtick={0.1, 1, 10, 100, 1000},
    xminorticks=true,
    xlabel={Frequency [Hz]},
    ymin=-200,
    ymax=200,
    ytick={-180,  -90,    0,   90,  180},
    ylabel={Phase [deg]},
    xminorgrids,
    legend style={at={(1,1.1)}, outer sep=2pt , anchor=north east, legend cell align=left, align=left, draw=black, nodes={scale=0.7, transform shape}},
    ]
    \addlegendimage{color=mycolor1, dashed, line width=1.5pt}
    \addlegendentry{$W_1^{-1}$};
    \addlegendimage{color=mycolor2, dashed, line width=1.5pt}
    \addlegendentry{$W_2^{-1}$};
    \addplot [color=mycolor1, line width=1.5pt]
    table [x=freqs, y=H1p, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_filters_results.csv};
    \addlegendentry{$H_1$};
    \addplot [color=mycolor2, line width=1.5pt]
    table [x=freqs, y=H2p, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_filters_results.csv};
    \addlegendentry{$H_2$};
  \end{axis}
\end{tikzpicture}

Figure 6: Frequency response of the weighting functions and complementary filters obtained using \(\mathcal{H}_\infty\) synthesis (png, pdf, tex).

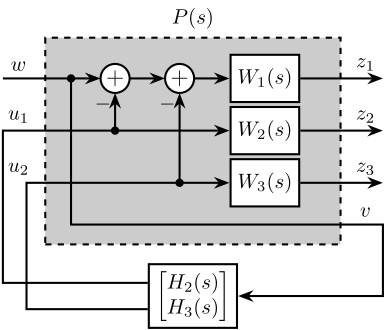
7 Fig 7: Architecture for \(\mathcal{H}_\infty\) synthesis of three complementary filters

\begin{tikzpicture}
   \node[block={5.0cm}{3.5cm}, fill=black!20!white, dashed] (P) {};
   \node[above] at (P.north) {$P(s)$};

   \coordinate[] (inputw)  at ($(P.south west)!0.8!(P.north west) + (-0.7, 0)$);
   \coordinate[] (inputu)  at ($(P.south west)!0.4!(P.north west) + (-0.7, 0)$);

   \coordinate[] (output1) at ($(P.south east)!0.8!(P.north east)  + (0.7, 0)$);
   \coordinate[] (output2) at ($(P.south east)!0.55!(P.north east) + (0.7, 0)$);
   \coordinate[] (output3) at ($(P.south east)!0.3!(P.north east)  + (0.7, 0)$);
   \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east)  + (0.7, 0)$);

   \node[block, left=1.4 of output1] (W1){$W_1(s)$};
   \node[block, left=1.4 of output2] (W2){$W_2(s)$};
   \node[block, left=1.4 of output3] (W3){$W_3(s)$};
   \node[addb={+}{}{}{}{-}, left=of W1] (sub1) {};
   \node[addb={+}{}{}{}{-}, left=of sub1] (sub2) {};

   \node[block, below=0.3 of P] (H) {$\begin{bmatrix}H_2(s) \\ H_3(s)\end{bmatrix}$};

   \draw[->] (inputw) node[above right](w){$w$} -- (sub2.west);
   \draw[->] (W3-|sub1)node[branch]{} -- (sub1.south);
   \draw[->] (W2-|sub2)node[branch]{} -- (sub2.south);
   \draw[->] ($(sub2.west)+(-0.5, 0)$) node[branch]{} |- (outputv) |- (H.east);
   \draw[->] ($(H.south west)!0.7!(H.north west)$) -| (inputu|-W2) -- (W2.west);
   \draw[->] ($(H.south west)!0.3!(H.north west)$) -| ($(inputu|-W3)+(0.4, 0)$) -- (W3.west);

   \draw[->] (sub2.east) -- (sub1.west);
   \draw[->] (sub1.east) -- (W1.west);
   \draw[->] (W1.east) -- (output1)node[above left](z){$z_1$};
   \draw[->] (W2.east) -- (output2)node[above left]{$z_2$};
   \draw[->] (W3.east) -- (output3)node[above left]{$z_3$};
   \node[above] at (W2-|w){$u_1$};
   \node[above] at (W3-|w){$u_2$};
   \node[above] at (outputv-|z){$v$};
\end{tikzpicture}

Figure 7: Architecture for \(\mathcal{H}_\infty\) synthesis of three complementary filters (png, pdf, tex).

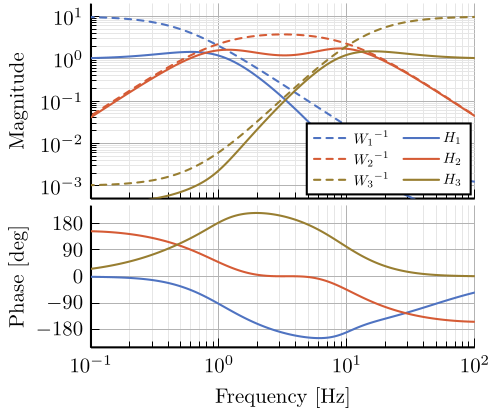
8 Fig 8: Frequency response of the weighting functions and three complementary filters obtained using \(\mathcal{H}_\infty\) synthesis

\setlength\fwidth{6.5cm}
\setlength\fheight{6cm}

\begin{tikzpicture}
  \begin{axis}[%
    width=1.0\fwidth,
    height=0.55\fheight,
    at={(0.0\fwidth, 0.42\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.1,
    xmax=100,
    xticklabels={{}},
    xminorticks=true,
    ymode=log,
    ymin=0.0005,
    ymax=20,
    ytick={0.001, 0.01, 0.1, 1, 10},
    yminorticks=true,
    ylabel={Magnitude},
    xminorgrids,
    yminorgrids,
    legend columns=2,
    legend style={
      /tikz/column 2/.style={
        column sep=5pt,
      },
      at={(1,0)}, outer sep=2pt , anchor=south east, legend cell align=left, align=left, draw=black, nodes={scale=0.7, transform shape}
    },
    ]
    \addplot [color=mycolor1, dashed, line width=1.5pt]
    table [x=freqs, y=W1, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_weights.csv};
    \addlegendentry{${W_1}^{-1}$};
    \addplot [color=mycolor1, line width=1.5pt]
    table [x=freqs, y=H1, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};
    \addlegendentry{$H_1$};


    \addplot [color=mycolor2, dashed, line width=1.5pt]
    table [x=freqs, y=W2, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_weights.csv};
    \addlegendentry{${W_2}^{-1}$};
    \addplot [color=mycolor2, line width=1.5pt]
    table [x=freqs, y=H2, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};
    \addlegendentry{$H_2$};

    \addplot [color=mycolor3, dashed, line width=1.5pt]
    table [x=freqs, y=W3, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_weights.csv};
    \addlegendentry{${W_3}^{-1}$};
    \addplot [color=mycolor3, line width=1.5pt]
    table [x=freqs, y=H3, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};
    \addlegendentry{$H_3$};
  \end{axis}

  \begin{axis}[%
    width=1.0\fwidth,
    height=0.4\fheight,
    at={(0.0\fwidth, 0.0\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.1,
    xmax=100,
    xminorticks=true,
    xlabel={Frequency [Hz]},
    ymin=-240,
    ymax=240,
    ytick={-180,  -90,    0,   90,  180},
    ylabel={Phase [deg]},
    xminorgrids,
    ]

    \addplot [color=mycolor1, line width=1.5pt]
    table [x=freqs, y=H1p, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};

    \addplot [color=mycolor2, line width=1.5pt]
    table [x=freqs, y=H2p, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};

    \addplot [color=mycolor3, line width=1.5pt]
    table [x=freqs, y=H3p, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/mathinf_three_results.csv};
  \end{axis}
\end{tikzpicture}

Figure 8: Frequency response of the weighting functions and three complementary filters obtained using \(\mathcal{H}_\infty\) synthesis (png, pdf, tex).

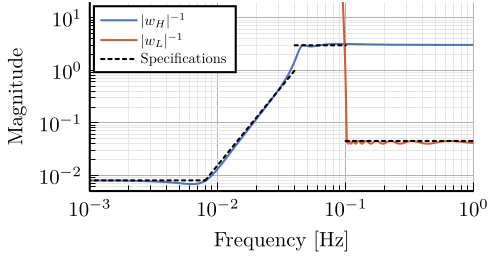
9 Fig 9: Specifications and weighting functions magnitude used for \(\mathcal{H}_\infty\) synthesis

\setlength\fwidth{6.5cm}
\setlength\fheight{3.2cm}

\begin{tikzpicture}
  \begin{axis}[%
    width=1.0\fwidth,
    height=1.0\fheight,
    at={(0.0\fwidth, 0.0\fheight)},
    scale only axis,
    separate axis lines,
    every outer x axis line/.append style={black},
    every x tick label/.append style={font=\color{black}},
    every x tick/.append style={black},
    xmode=log,
    xmin=0.001,
    xmax=1,
    xminorticks=true,
    xlabel={Frequency [Hz]},
    every outer y axis line/.append style={black},
    every y tick label/.append style={font=\color{black}},
    every y tick/.append style={black},
    ymode=log,
    ymin=0.005,
    ymax=20,
    yminorticks=true,
    ylabel={Magnitude},
    axis background/.style={fill=white},
    xmajorgrids,
    xminorgrids,
    ymajorgrids,
    yminorgrids,
    legend style={at={(0,1)}, outer sep=2pt, anchor=north west, legend cell align=left, align=left, draw=black, nodes={scale=0.7, transform shape}}
    ]

    \addplot [color=mycolor1, line width=1.5pt]
      table [x=freqs, y=wHm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matligo_weights.csv};
    \addlegendentry{$|w_H|^{-1}$}

    \addplot [color=mycolor2, line width=1.5pt]
      table [x=freqs, y=wLm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matligo_weights.csv};
    \addlegendentry{$|w_L|^{-1}$}

    \addplot [color=black, dotted, line width=1.5pt]
    table[row sep=crcr]{%
      0.0005    0.008\\
      0.008   0.008\\
    };
    \addlegendentry{Specifications}

    \addplot [color=black, dotted, line width=1.5pt, forget plot]
    table[row sep=crcr]{%
      0.008 0.008\\
      0.04  1\\
    };
    \addplot [color=black, dotted, line width=1.5pt, forget plot]
    table[row sep=crcr]{%
      0.04  3\\
      0.1   3\\
    };
    \addplot [color=black, dotted, line width=1.5pt]
    table[row sep=crcr]{%
      0.1   0.045\\
      2   0.045\\
    };
  \end{axis}
\end{tikzpicture}

Figure 9: Specifications and weighting functions magnitude used for \(\mathcal{H}_\infty\) synthesis (png, pdf, tex).

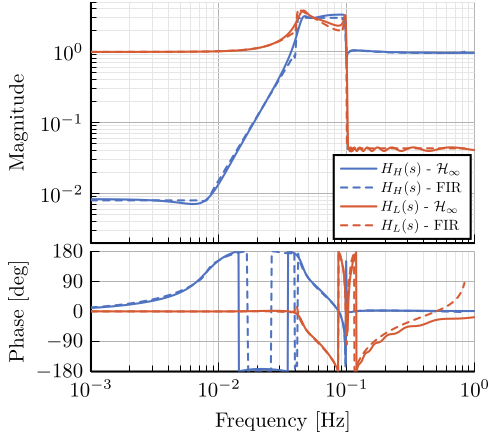
10 Fig 10: Comparison of the FIR filters (solid) with the filters obtained with \(\mathcal{H}_\infty\) synthesis (dashed)

\setlength\fwidth{6.5cm}
\setlength\fheight{6.8cm}

\begin{tikzpicture}
  \begin{axis}[%
    width=1.0\fwidth,
    height=0.60\fheight,
    at={(0.0\fwidth, 0.32\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.001,
    xmax=1,
    xtick={0.001,0.01,0.1,1},
    xticklabels={{}},
    xminorticks=true,
    ymode=log,
    ymin=0.002,
    ymax=5,
    ytick={0.001, 0.01, 0.1, 1, 10},
    yminorticks=true,
    ylabel={Magnitude},
    xminorgrids,
    yminorgrids,
    legend style={at={(1,0)}, outer sep=2pt, anchor=south east, legend cell align=left, align=left, draw=black, nodes={scale=0.7, transform shape}}
    ]
    \addplot [color=mycolor1, line width=1.5pt]
      table [x=freqs, y=Hhm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_hinf.csv};
    \addlegendentry{$H_H(s)$ - $\mathcal{H}_\infty$}
    \addplot [color=mycolor1, dashed, line width=1.5pt]
      table [x=freqs, y=Hhm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_fir.csv};
    \addlegendentry{$H_H(s)$ - FIR}
    \addplot [color=mycolor2, line width=1.5pt]
      table [x=freqs, y=Hlm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_hinf.csv};
    \addlegendentry{$H_L(s)$ - $\mathcal{H}_\infty$}
    \addplot [color=mycolor2, dashed, line width=1.5pt]
      table [x=freqs, y=Hlm, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_fir.csv};
    \addlegendentry{$H_L(s)$ - FIR}
  \end{axis}

  \begin{axis}[%
    width=1.0\fwidth,
    height=0.3\fheight,
    at={(0.0\fwidth, 0.0\fheight)},
    scale only axis,
    xmode=log,
    xmin=0.001,
    xmax=1,
    xtick={0.001,  0.01,   0.1,     1},
    xminorticks=true,
    xlabel={Frequency [Hz]},
    ymin=-180,
    ymax=180,
    ytick={-180,  -90,    0,   90,  180},
    ylabel={Phase [deg]},
    xminorgrids,
    ]
    \addplot [color=mycolor1, line width=1.5pt, forget plot]
      table [x=freqs, y=Hhp, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_hinf.csv};
    \addplot [color=mycolor1, dashed, line width=1.5pt, forget plot]
      table [x=freqs, y=Hhp, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_fir.csv};
    \addplot [color=mycolor2, line width=1.5pt, forget plot]
      table [x=freqs, y=Hlp, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_hinf.csv};
    \addplot [color=mycolor2, dashed, line width=1.5pt, forget plot]
      table [x=freqs, y=Hlp, col sep=comma] {/home/thomas/Cloud/thesis/papers/dehaeze19_desig_compl_filte/matlab/matcomp_ligo_fir.csv};
  \end{axis}
\end{tikzpicture}

Figure 10: Comparison of the FIR filters (solid) with the filters obtained with \(\mathcal{H}_\infty\) synthesis (dashed) (png, pdf, tex).