Huddle Test of the L22 Geophones
Table of Contents
- 1. Experimental Setup
- 2. Signal Processing
- 2.1. Load data
- 2.2. Time Domain Data
- 2.3. Computation of the ASD of the measured voltage
- 2.4. Scaling to take into account the sensibility of the geophone and the voltage amplifier
- 2.5. Computation of the ASD of the velocity
- 2.6. Transfer function between the two geophones
- 2.7. Estimation of the sensor noise
- 3. Compare axis
- 4. Appendix
1 Experimental Setup
Two L22 geophones are used. They are placed on the ID31 granite. They are leveled.
The signals are amplified using voltage amplifier with a gain of 60dB. The voltage amplifiers includes:
- an high pass filter with a cut-off frequency at 1.5Hz (AC option)
- a low pass filter with a cut-off frequency at 1kHz

Figure 1: Setup

Figure 2: Geophones
2 Signal Processing
All the files (data and Matlab scripts) are accessible here.
2.1 Load data
We load the data of the z axis of two geophones.
load('mat/data_001.mat', 't', 'x1', 'x2'); dt = t(2) - t(1);
2.2 Time Domain Data
figure; hold on; plot(t, x1); plot(t, x2); hold off; xlabel('Time [s]'); ylabel('Voltage [V]'); xlim([t(1), t(end)]);
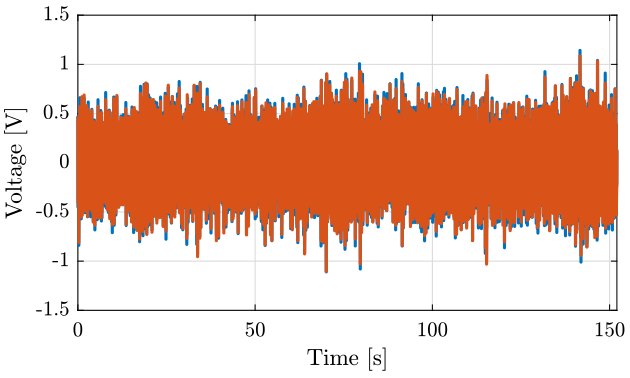
Figure 3: Time domain Data
figure; hold on; plot(t, x1); plot(t, x2); hold off; xlabel('Time [s]'); ylabel('Voltage [V]'); xlim([0 1]);
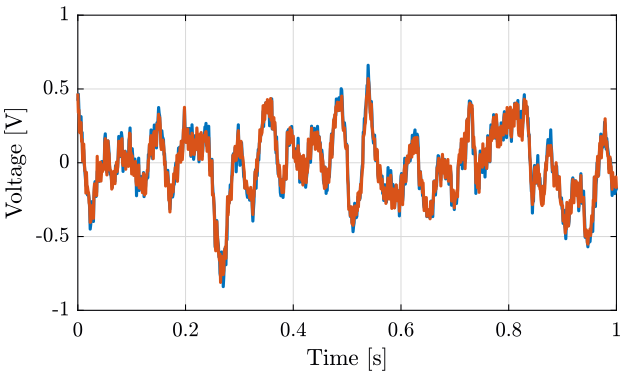
Figure 4: Time domain Data - Zoom
2.3 Computation of the ASD of the measured voltage
We first define the parameters for the frequency domain analysis.
Fs = 1/dt; % [Hz] win = hanning(ceil(10*Fs));
Then we compute the Power Spectral Density using pwelch function.
[pxx1, f] = pwelch(x1, win, [], [], Fs);
[pxx2, ~] = pwelch(x2, win, [], [], Fs);
And we plot the result on figure 5.
figure; hold on; plot(f, sqrt(pxx1)); plot(f, sqrt(pxx2)); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$') xlim([0.1, 500]);
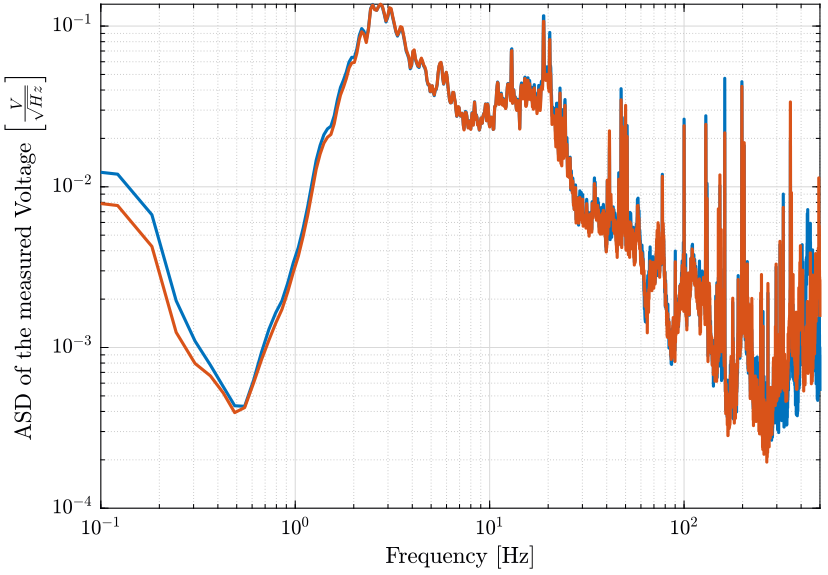
Figure 5: Amplitude Spectral Density of the measured voltage
2.4 Scaling to take into account the sensibility of the geophone and the voltage amplifier
The Geophone used are L22. Their sensibility is shown on figure 6.
S0 = 88; % Sensitivity [V/(m/s)] f0 = 2; % Cut-off frequnecy [Hz] S = S0*(s/2/pi/f0)/(1+s/2/pi/f0);
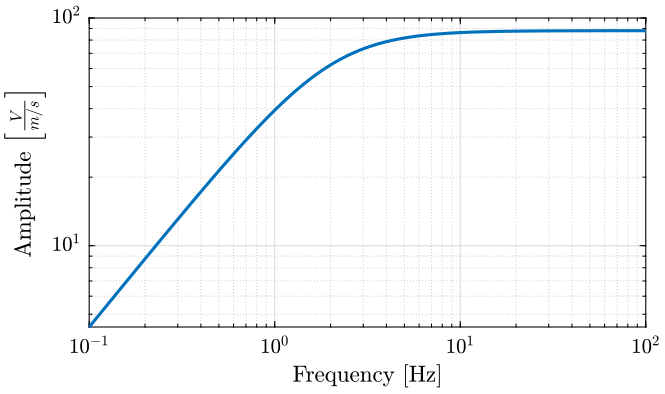
Figure 6: Sensibility of the Geophone
We also take into account the gain of the electronics which is here set to be \(60dB\).
G0_db = 60; % [dB] G0 = 10^(G0_db/20); % [abs]
We divide the ASD measured (in \(\text{V}/\sqrt{\text{Hz}}\)) by the gain of the voltage amplifier to obtain the ASD of the voltage across the geophone. We further divide the result by the sensibility of the Geophone to obtain the ASD of the velocity in \(m/s/\sqrt{Hz}\).
scaling = 1./squeeze(abs(freqresp(G0*S, f, 'Hz')));
2.5 Computation of the ASD of the velocity
The ASD of the measured velocity is shown on figure 7.
figure; hold on; plot(f, sqrt(pxx1).*scaling); plot(f, sqrt(pxx2).*scaling); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD of the measured Velocity $\left[\frac{m/s}{\sqrt{Hz}}\right]$') xlim([0.1, 500]);
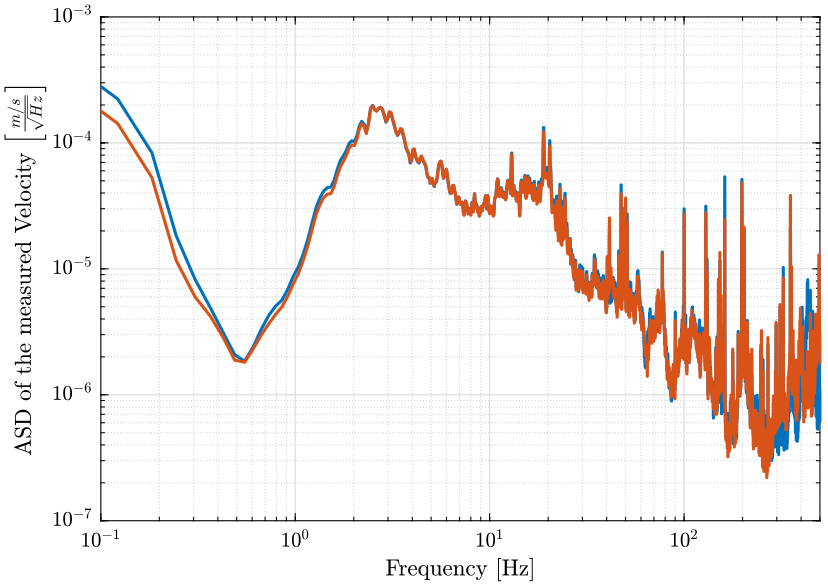
Figure 7: Amplitude Spectral Density of the Velocity
We also plot the ASD in displacement (figure 8);
figure; hold on; plot(f, (sqrt(pxx1).*scaling)./(2*pi*f)); plot(f, (sqrt(pxx2).*scaling)./(2*pi*f)); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD of the displacement $\left[\frac{m}{\sqrt{Hz}}\right]$') xlim([0.1, 500]);
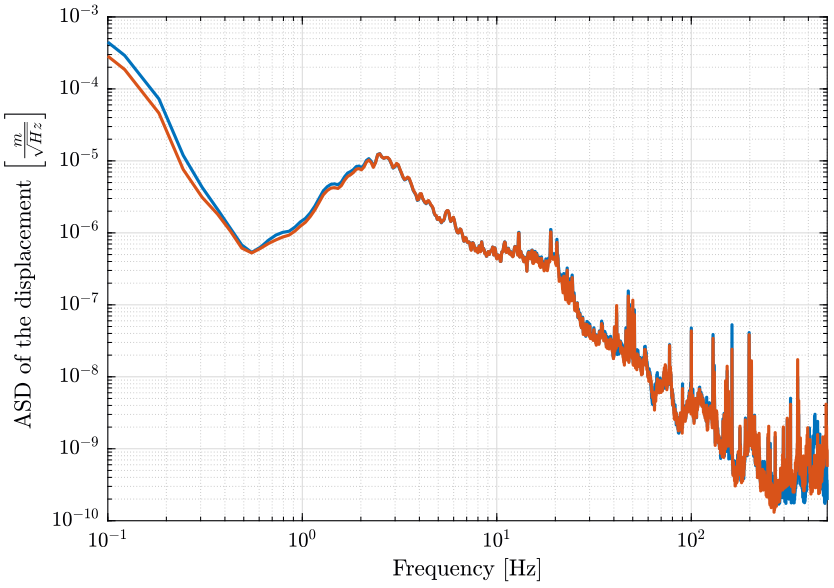
Figure 8: Amplitude Spectral Density of the Displacement
2.6 Transfer function between the two geophones
We here compute the transfer function from one geophone to the other. The result is shown on figure 9.
We also compute the coherence between the two signals (figure 10).
[T12, ~] = tfestimate(x1, x2, win, [], [], Fs);
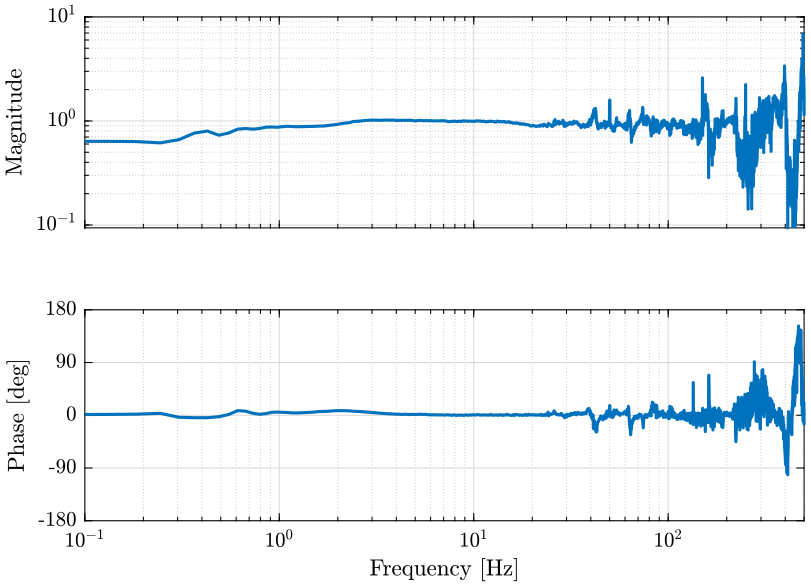
Figure 9: Estimated transfer function between the two geophones
[coh12, ~] = mscohere(x1, x2, win, [], [], Fs);
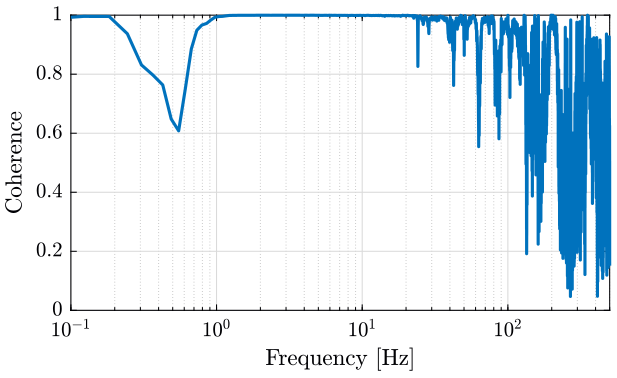
Figure 10: Cohererence between the signals of the two geophones
2.7 Estimation of the sensor noise
The technique to estimate the sensor noise is taken from (Barzilai, VanZandt, and Kenny 1998).
The coherence between signals \(X\) and \(Y\) is defined as follow \[ \gamma^2_{XY}(\omega) = \frac{|G_{XY}(\omega)|^2}{|G_{X}(\omega)| |G_{Y}(\omega)|} \] where \(|G_X(\omega)|\) is the output Power Spectral Density (PSD) of signal \(X\) and \(|G_{XY}(\omega)|\) is the Cross Spectral Density (CSD) of signal \(X\) and \(Y\).
The PSD and CSD are defined as follow:
\begin{align} |G_X(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} \left| X_k(\omega, T) \right|^2 \\ |G_{XY}(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} [ X_k^*(\omega, T) ] [ Y_k(\omega, T) ] \end{align}where:
- \(n_d\) is the number for records averaged
- \(T\) is the length of each record
- \(X_k(\omega, T)\) is the finite Fourier transform of the kth record
- \(X_k^*(\omega, T)\) is its complex conjugate
The mscohere function is compared with this formula on Appendix (section 4.1), it is shown that it is identical.
Figure 11 illustrate a block diagram model of the system used to determine the sensor noise of the geophone.
Two geophones are mounted side by side to ensure that they are exposed by the same motion input \(U\).
Each sensor has noise \(N\) and \(M\).
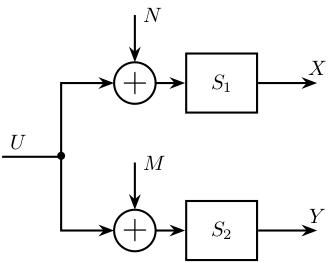
Figure 11: Huddle test block diagram
We here assume that each sensor has the same magnitude of instrumental noise: \(N = M\). We also assume that \(S_1 = S_2 = 1\).
We then obtain:
\begin{equation} \label{orgbacdde9} \gamma_{XY}^2(\omega) = \frac{1}{1 + 2 \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right) + \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right)^2} \end{equation}Since the input signal \(U\) and the instrumental noise \(N\) are incoherent:
\begin{equation} \label{org21035bd} |G_X(\omega)| = |G_N(\omega)| + |G_U(\omega)| \end{equation}From equations \eqref{orgbacdde9} and \eqref{org21035bd}, we finally obtain
The instrumental noise is computed below. The result in V^2/Hz is shown on figure 12.
pxxN = pxx1.*(1 - coh12);
figure; hold on; plot(f, pxx1, '-'); plot(f, pxx2, '-'); plot(f, pxxN, 'k--'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('PSD of the measured Voltage $\left[\frac{V^2}{Hz}\right]$'); xlim([0.1, 500]);
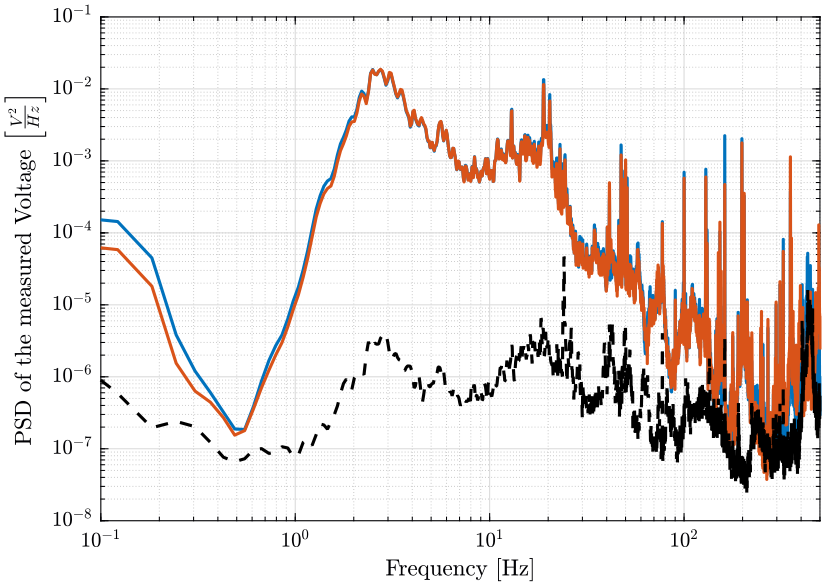
Figure 12: Instrumental Noise and Measurement in \(V^2/Hz\)
This is then further converted into velocity and compared with the ground velocity measurement. (figure 13)
figure; hold on; plot(f, sqrt(pxx1).*scaling, '-'); plot(f, sqrt(pxx2).*scaling, '-'); plot(f, sqrt(pxxN).*scaling, 'k--'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD of the Velocity $\left[\frac{m/s}{\sqrt{Hz}}\right]$'); xlim([0.1, 500]);
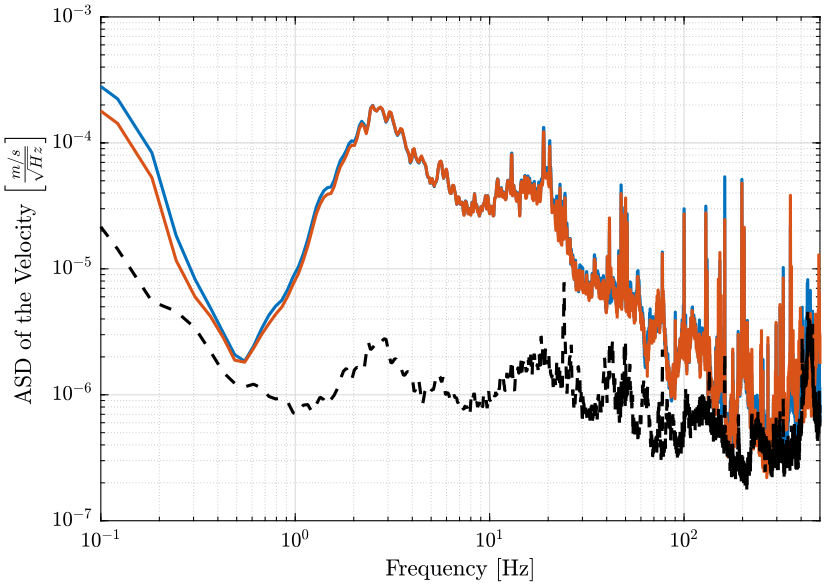
Figure 13: Instrumental Noise and Measurement in \(m/s/\sqrt{Hz}\)
3 Compare axis
All the files (data and Matlab scripts) are accessible here.
3.1 Load data
We first load the data for the three axis.
z = load('mat/data_001.mat', 't', 'x1', 'x2'); east = load('mat/data_002.mat', 't', 'x1', 'x2'); north = load('mat/data_003.mat', 't', 'x1', 'x2');
3.2 Compare PSD
The PSD for each axis of the two geophones are computed.
[pz1, fz] = pwelch(z.x1, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1))); [pz2, ~] = pwelch(z.x2, hanning(ceil(length(z.x2)/100)), [], [], 1/(z.t(2)-z.t(1))); [pe1, fe] = pwelch(east.x1, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1))); [pe2, ~] = pwelch(east.x2, hanning(ceil(length(east.x2)/100)), [], [], 1/(east.t(2)-east.t(1))); [pn1, fn] = pwelch(north.x1, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1))); [pn2, ~] = pwelch(north.x2, hanning(ceil(length(north.x2)/100)), [], [], 1/(north.t(2)-north.t(1)));
We compare them. The result is shown on figure 14.
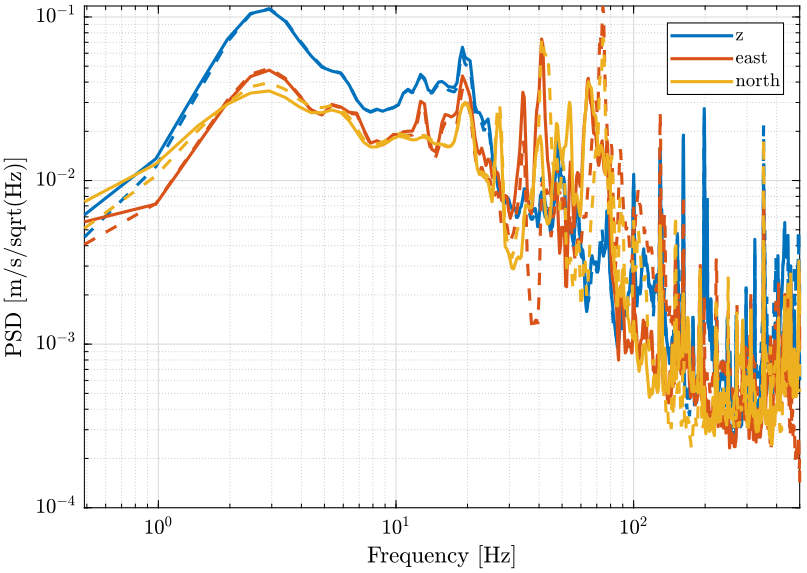
Figure 14: Compare the measure PSD of the two geophones for the three axis
3.3 Compare TF
The transfer functions from one geophone to the other are also computed for each axis. The result is shown on figure 15.
[Tz, fz] = tfestimate(z.x1, z.x2, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1))); [Te, fe] = tfestimate(east.x1, east.x2, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1))); [Tn, fn] = tfestimate(north.x1, north.x2, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1)));
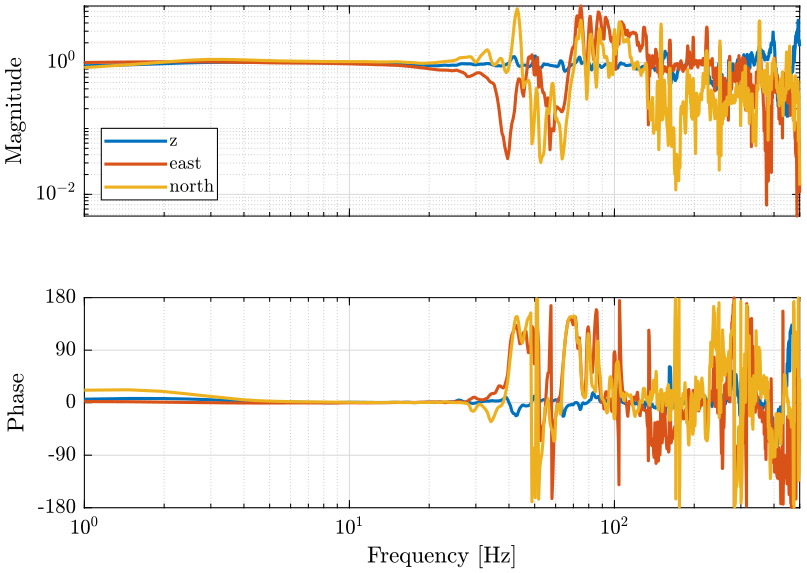
Figure 15: Compare the transfer function from one geophone to the other for the 3 axis
4 Appendix
4.1 Computation of coherence from PSD and CSD
load('mat/data_001.mat', 't', 'x1', 'x2'); dt = t(2) - t(1); Fs = 1/dt; win = hanning(ceil(length(x1)/100));
pxy = cpsd(x1, x2, win, [], [], Fs); pxx = pwelch(x1, win, [], [], Fs); pyy = pwelch(x2, win, [], [], Fs); coh = mscohere(x1, x2, win, [], [], Fs);
figure; hold on; plot(f, abs(pxy).^2./abs(pxx)./abs(pyy), '-'); plot(f, coh, '--'); hold off; set(gca, 'xscale', 'log'); xlabel('Frequency'); ylabel('Coherence'); xlim([1, 500]);
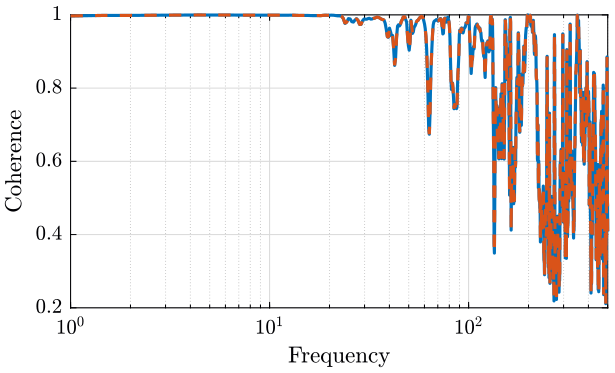
Figure 16: Comparison of mscohere and manual computation